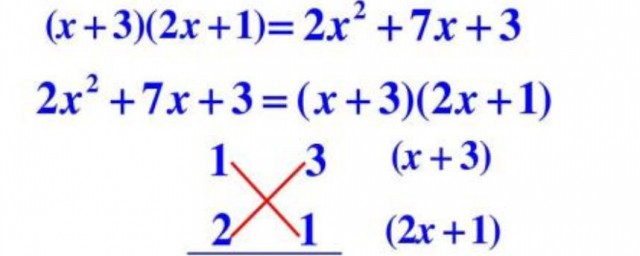
1、十字分解法的方法簡單來講就是:十字左邊相乘等於二次項,右邊相乘等於常數項,交叉相乘再相加等於一次項系數。其實就是運用乘法公式運算來進行因式分解。
2、十字分解法能用於二次三項式(一元二次式)的分解因式(不一定是整數范圍內)。對於像ax2+bx+c=(a1x+c1)(a2x+c2)這樣的整式來說,這個方法的關鍵是把二次項系數a分解成兩個因數a1,a2的積,把常數項c分解成兩個因數c1,c2的積,並使a1c2+a2c1正好等於一次項的系數b。那麼可以直接寫成結果:ax2+bx+c=(a1x+c1)(a2x+c2)。在運用這種方法分解因式時,要註意觀察,嘗試,並體會,它的實質是二項式乘法的逆過程。當首項系數不是1時,往往需要多次試驗,務必註意各項系數的符號。基本式子:x2+(p+q)x+pq=(x+p)(x+q)。
3、示例:
(1)例1因式分解:x2-x-56;
分析:因為7x+(-8x)=-x;
解:原式=(x+7)(x-8)。
(2)例2因式分解:x2-10x+16;
分析:因為-2x+(-8x)=-10x;
解:原式=(x-2)(x-8)。













