2、SAS(邊角邊),即三角形的其中兩條邊對應相等,且兩條邊的夾角也對應相等的兩個三角形全等。
舉例:如下圖,AB平分∠CAD,AC=AD,求證∠C=∠D.證明:∵AB平分∠CAD.∴∠CAB=∠BAD.在△ACB與△ADB中{AC=AD,∠CAB=∠BAD,AB=AB.∴△ACB≌△ADB.(SAS)∴∠C=∠D.(全等三角形的對應角相等)。
3、ASA(角邊角),即三角形的其中兩個角對應相等,且兩個角夾的的邊也對應相等的兩個三角形全等。
舉例:如下圖,AB=AC,∠B=∠C,求證△ABE≌△ACD.證明:在△ABE與△ACD中{∠A=∠A,AB=AC,∠B=∠C.∴△ABE≌△ACD.(ASA)。
4、AAS(角角邊),即三角形的其中兩個角對應相等,且對應相等的角所對應的邊也對應相等的兩個三角形全等。
舉例:如下圖,AB=DE,∠A=∠E,求證∠B=∠D.證明:在△ABC與△EDC中{∠A=∠E,∠ACB=∠DCE,AB=DE.∴△ABC≌△EDC.(AAS)∴∠B=∠D.(全等三角形的對應角相等)。
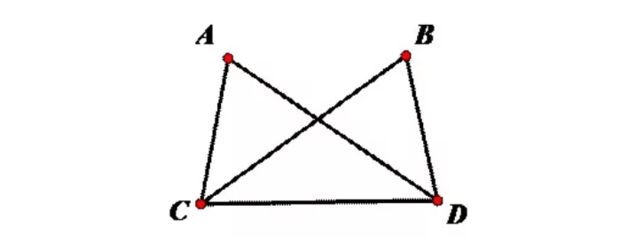
5、HL(斜邊、直角邊),即在直角三角形中一條斜邊和一條直角邊對應相等的兩個直角三角形全等。
舉例:如下圖,Rt△ADC與Rt△BCD,AC=BD,求證AD=BC.
證明:在Rt△ADC與Rt△BCD中{AC=BD,CD=CD.∴Rt△ADC與Rt△BCD.(HL)∴AD=BC.(全等三角形的對應邊相等)。



















