多邊形的外角和 多邊形的外角和介紹

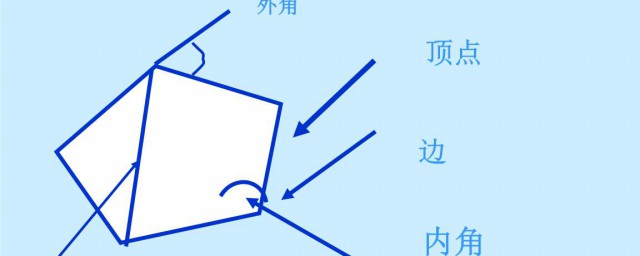
1、多邊形的外角和是360度。

2、證明過程如下：設多邊形的邊數為n，則其內角和＝（n-2）*180°，因為n邊形有n個頂點，每個頂點的一個外角和相鄰的內角互補，等於180°，所以n邊形的外角和等於n*180°-（n-2）*180°等於360°，即n邊形的外角和等於360度。